Using a Surrogate Tree Explainer

This example illustrates how to use a tabular surrogate tree-based explainer to explain a prediction.

This example shows how to use the tabular surrogate tree-based explainer implementation – fatf.transparency.predictions.surrogate_explainers.TabularBlimeyTree – to explain a prediction of a black-box probabilistic model.

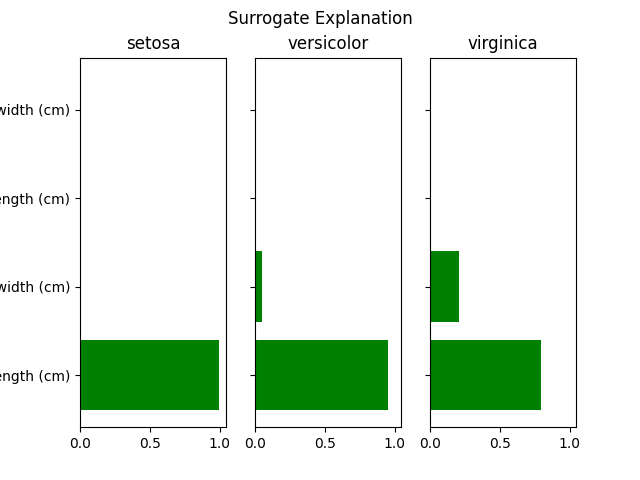
Out:

{'setosa': {'petal length (cm)': 0.9947582385676036,
            'petal width (cm)': 0.0,
            'sepal length (cm)': 0.0,
            'sepal width (cm)': 0.00524176143239636},
 'versicolor': {'petal length (cm)': 0.9496406928798405,
                'petal width (cm)': 0.05035930712015947,
                'sepal length (cm)': 0.0,
                'sepal width (cm)': 0.0},
 'virginica': {'petal length (cm)': 0.7962708998702057,
               'petal width (cm)': 0.20372910012979428,
               'sepal length (cm)': 0.0,
               'sepal width (cm)': 0.0}}

# Author: Kacper Sokol <k.sokol@bristol.ac.uk>
# License: new BSD

from pprint import pprint

import fatf

import fatf.utils.data.datasets as fatf_datasets
import fatf.utils.models as fatf_models

import fatf.transparency.predictions.surrogate_explainers as fatf_surrogates

import fatf.vis.lime as fatf_vis_lime

print(__doc__)

# Fix random seed
fatf.setup_random_seed(42)

# Load data
iris_data_dict = fatf_datasets.load_iris()
iris_X = iris_data_dict['data']
iris_y = iris_data_dict['target']
iris_feature_names = iris_data_dict['feature_names'].tolist()
iris_class_names = iris_data_dict['target_names'].tolist()

# Train a model
clf = fatf_models.KNN()
clf.fit(iris_X, iris_y)

# Create a LIME explainer
tree = fatf_surrogates.TabularBlimeyTree(
    iris_X,
    clf,
    feature_names=iris_feature_names,
    class_names=iris_class_names)

# Choose an index of the instance to be explained
index_to_explain = 42

# Explain an instance
tree_explanation = tree.explain_instance(
    iris_X[index_to_explain, :], samples_number=500)

# Display the textual explanation
pprint(tree_explanation)

# Plot the explanation
fatf_vis_lime.plot_lime(tree_explanation)